Regressão Linear - Parâmetros

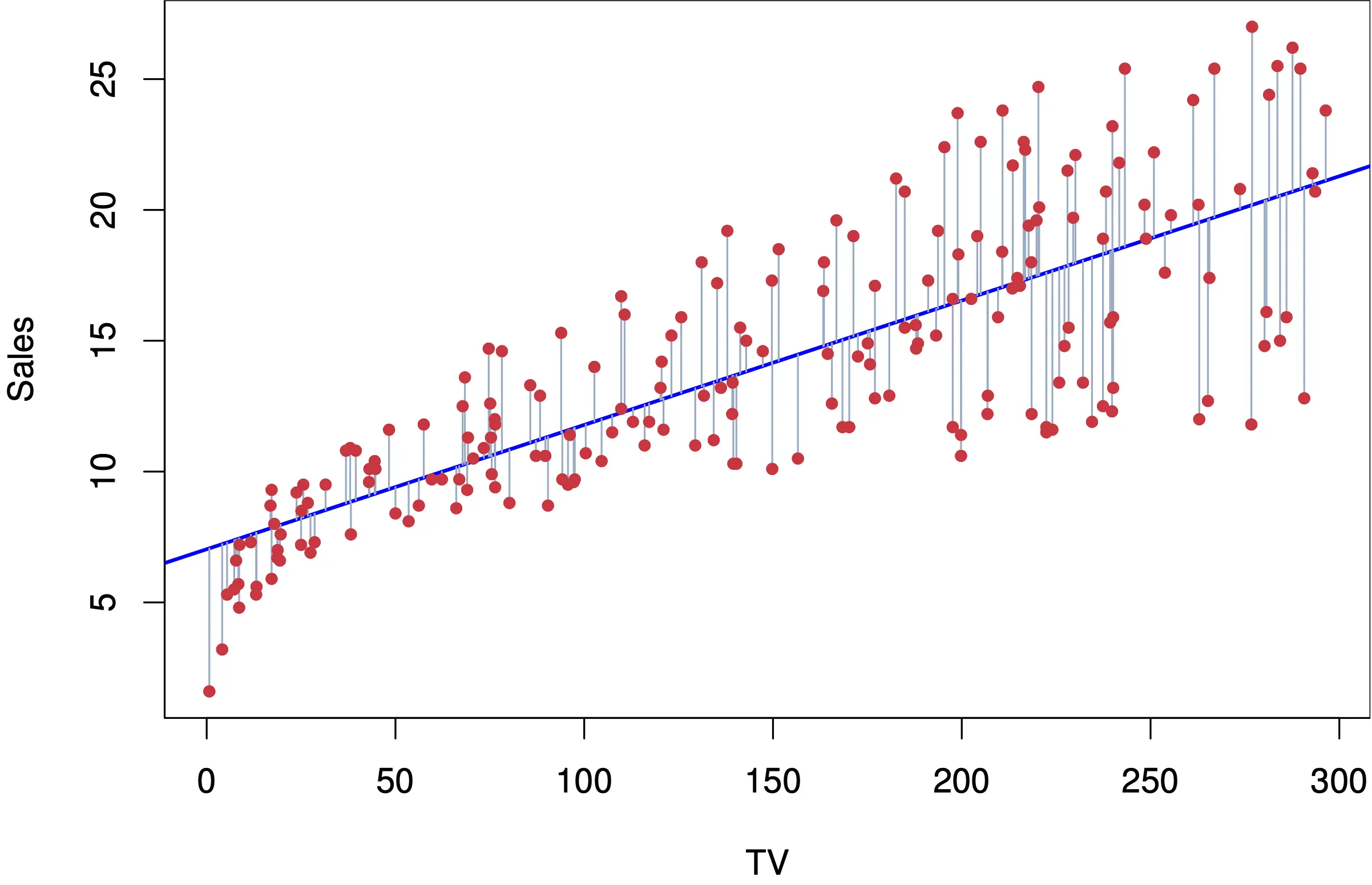
Para realizar uma regressão linear simples usando o método dos Mínimos Quadrados Ordinários (MQO), buscamos minimizar a soma dos quadrados dos erros $S$:

$$S = \sum_{i=1}^{n} (Y_{i} - \hat{Y}_{i})^2$$

Onde:

• $Y_{i}$ é o valor observado da variável dependente.
• $\hat{Y}_{i}$ é o valor predito da variável dependente.

Intercepto da equação $(\hat{b}_{0})$

Para encontrar os coeficientes que minimizam o erro, começamos com a derivada parcial de $S$ em relação a $\hat{b}_{0}$ e igualamos a zero:

$$\frac{\partial S}{\partial b_{0}} = \sum_{i=1}^{n} 2(Y_{i} - b_{0} - b_{1}X_{i})(-1)$$

Aplicando a regra da cadeia na derivada:

$$-2 \sum_{i=1}^{n} (Y_{i} - b_{0} - b_{1}X_{i}) = 0$$

Dividimos ambos os lados por -2:

$$\sum_{i=1}^{n} (Y_{i} - b_{0} - b_{1}X_{i}) = 0$$

Propriedades importantes a serem recordadas:

1. A média dos valores observados de $Y$:

$$\overline{Y} = \frac{1}{n} \sum_{i=1}^{n} Y_{i}$$

2. A soma dos valores observados de $Y$:

$$\sum_{i=1}^{n} Y_{i} = n\overline{Y}$$

3. A soma dos valores observados de $X$:

$$\sum_{i=1}^{n} X_{i} = n\overline{X}$$

4. A variância de $X$:

$$\sum_{i=1}^{n} (X_{i} - \overline{X})^2 = \sum_{i=1}^{n} X_{i}^2 - n\overline{X}^2$$

Continuando com o desenvolvimento da equação:

$$\sum_{i=1}^{n} (Y_{i} - b_{0} - b_{1}X_{i}) = 0$$ $$\sum_{i=1}^{n} Y_{i} - \sum_{i=1}^{n} b_{0} - \sum_{i=1}^{n} b_{1}X_{i} = 0$$

Utilizando as propriedades 2 e 3:

$$n\overline{Y} - nb_{0} - b_{1}n\overline{X} = 0$$

Dividindo ambos os lados por $n$:

$$\overline{Y} - b_{0} - b_{1}\overline{X} = 0$$

Portanto, o intercepto (ou coeficiente $b_{0}$) é:

$$\hat{b}_{0} = \overline{Y} - b_{1}\overline{X}$$

Coeficiente Angular $(\hat{b}_{1})$

Para a inclinação (ou coeficiente angular), necessitamos da derivada parcial em relação a $b_{1}$:

$$\frac{\partial S}{\partial b_{1}} = \sum_{i=1}^{n} 2(Y_{i} - b_{0} - b_{1}X_{i})(-X_{i})$$

Dividimos ambos os lados por $-2$:

$$\sum_{i=1}^{n} (Y_{i} - b_{0} - b_{1}X_{i})X_{i} = 0$$

Desenvolvendo a equação:

$$\sum_{i=1}^{n} (X_{i}Y_{i} - b_{0}X_{i} - b_{1}X_{i}^2) = 0$$ $$\sum_{i=1}^{n} X_{i}Y_{i} - b_{0}\sum_{i=1}^{n} X_{i} - b_{1}\sum_{i=1}^{n} X_{i}^2 = 0$$

Utilizando as propriedades e a equação do intercepto:

$$\sum_{i=1}^{n} X_{i}Y_{i} - n\overline{X}\overline{Y} + b_{1}n\overline{X}^2 - b_{1}\sum_{i=1}^{n} X_{i}^2 = 0$$

Aplicando a última propriedade (variância de $X$):

$$\sum_{i=1}^{n} (X_{i} - \overline{X})(Y_{i} - \overline{Y}) = b_{1} \sum_{i=1}^{n} (X_{i} - \overline{X})^2$$

Portanto, o coeficiente angular (ou inclinação) é:

$$\hat{b}_{1} = \frac{\sum_{i=1}^{n} (X_{i} - \overline{X})(Y_{i} - \overline{Y})}{\sum_{i=1}^{n} (X_{i} - \overline{X})^2}$$