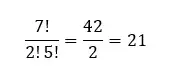Pascal e Covariância

Quando calculamos, por exemplo, a variância de um portfólio de 3 ativos temos que considerar a covariância única entre os ativos

Para o portfólio composto pelos ativos A, B e C necessitariamos da Cov(A,B); Cov(A,C) e Cov(B,C) — Total de 3 termos únicos de covariância

Para 4 ativos — Cov (A,B); Cov(A,C); Cov (A,D); Cov (B,C) ; Cov (B,D); Cov (C,D) = 6 termos únicos

Agora note o triângulo de Pascal:

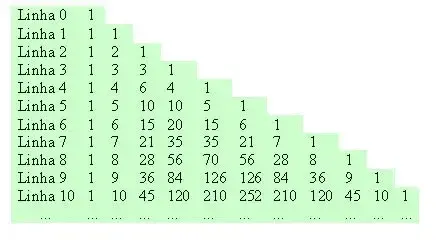
O elemento número x da linha n em um triângulo de Paschal pode ser descrito pela seguinte fórmula:

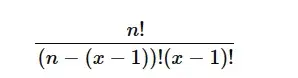
Percebeu alguma relação na imagem abaixo?

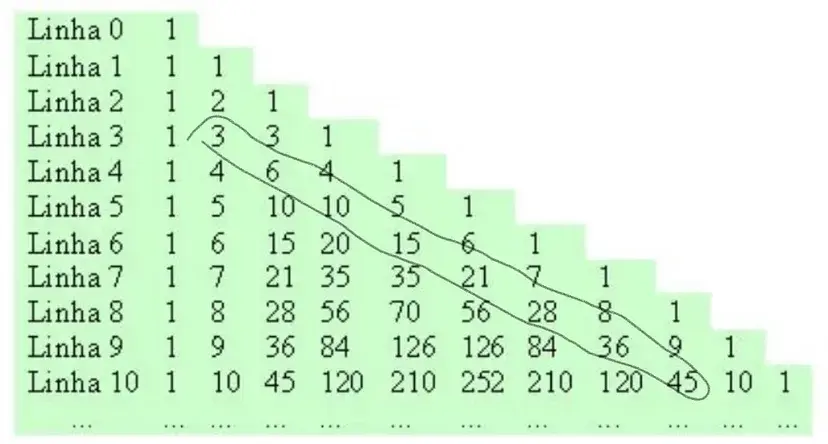
Para um portfólio de n ativos (linha n), podemos dizer que a quantidade única de termos de covariância é o elemento n-1

Substituindo na fórmula inicial, teriamos que:

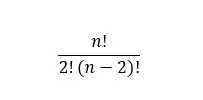
Logo, para um portfólio de 7 ativos, teriamos 21 termos únicos, e assim por diante.