Erro Padrão

O conceito de erro padrão e sua importância na inferência estatística

Jean Victor Estatística

Apr 18, 2024

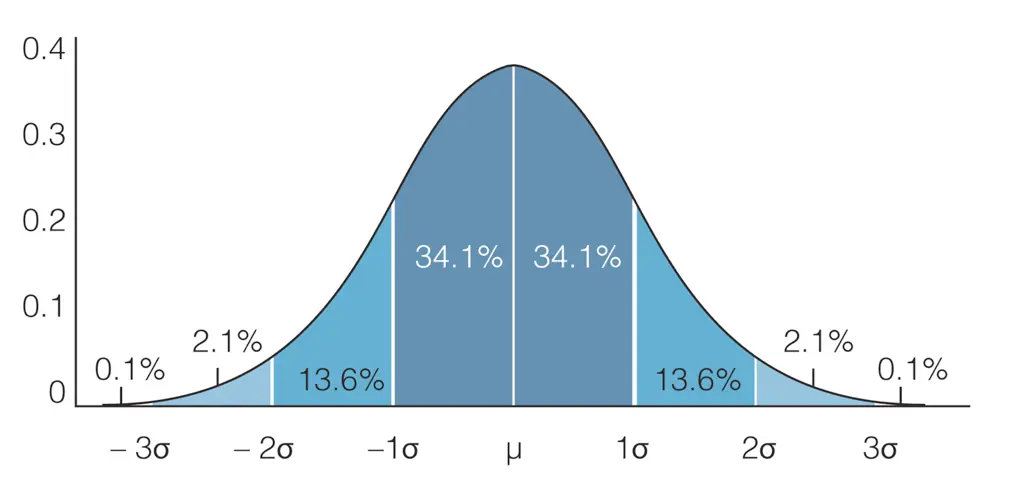
O Teorema Central do Limite afirma que, para uma amostra grande o suficiente, a distribuição da média amostral tende a ser aproximadamente normal.

O erro padrão nos fornece a ideia de quão distante, em média, nossa estimativa a partir da amostra está da verdadeira média populacional.

Considerando uma variável aleatória $X$ , temos que sua variância é dada pela fórmula:

V A R (X) = E ([X - E (X)]^{2})

Para a variância de $X$ atribuindo-se uma constante $a$ multiplicando o valor daquela:

V A R (a X) = E ([a X - E (a X)]^{2})

V A R (a X) = E ([a X - a E (X)]^{2})

V A R (a X) = E ([a (X - E (X))]^{2})

V A R (a X) = E (a^{2} (X - E (X))^{2})

V A R (a X) = a^{2} E (X - E (X))^{2}

∴ V A R (a X) = a^{2} V A R (X)

A variância da média amostral pode ser dada por:

V A R (\overset{―}{X}) = V A R (\frac{X_{1} + X_{2} + X_{3} + \dots + X_{n}}{n})

V A R (\overset{―}{X}) = V A R (\frac{1}{n} [X_{1} + X_{2} + X_{3} + \dots + X_{n}])

Utilizando a propriedade desenvolvida anteriormente, temos que:

V A R (\overset{―}{X}) = \frac{1}{n^{2}} V A R (X_{1} + X_{2} + X_{3} + \dots + X_{n})

V A R (\overset{―}{X}) = \frac{1}{n^{2}} [n S^{2}]

V A R (\overset{―}{X}) = \frac{S^{2}}{n}

∴ S D (\overset{―}{X}) = \frac{S}{\sqrt{n}}

De tal modo, obtemos a fórmula do erro padrão, instrumento de suma importância para o cálculo do intervalo de confiança (como pode ser observado abaixo, com a definição do valor $z$ para o nível de confiança desejado e seu produto com o erro padrão, temos o que se chama comumente de margem de erro):

I C = \overset{―}{X} \pm z \frac{σ}{\sqrt{n}}

No caso do desvio padrão da população ser desconhecido, utilizamos o valor $t$ de Student e o desvio padrão amostral:

I C = \overset{―}{X} \pm t \frac{S}{\sqrt{n}}

I C = \overset{―}{X} \pm margem de erro

O intervalo de confiança é uma estimativa de intervalo que é construída com base na média amostral e na margem de erro para inferir sobre a média populacional com um determinado nível de confiança.